A Mathematical Gem :: Euler's Identity

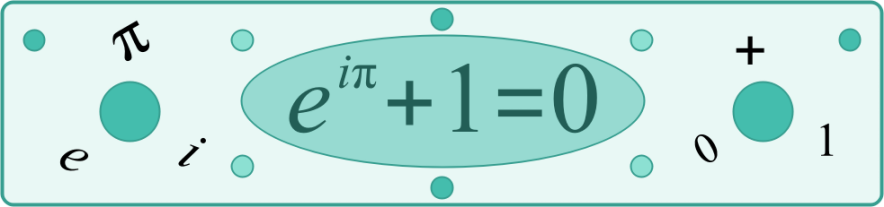
Euler's Identity is one of the most beautiful equations in the field of Mathemetics, which is a combination of five constants - $e$, $i$, $\pi$, $1$, and $0$ !!!

In mathematical terms, the Euler's Identity equation is expressed as follows:

$e^{i\pi} + 1 = 0$

where

$e$ is a constant that equals to $2.718.....$,

$i$ is the imaginary unit such that $i^2$ equals to $-1$,

and $\pi$ is a constant that equals to $3.141.....$.

Let us now try to prove the Euler's Identity equation.

A prerequisite for the proof - one must have a good grasp of Derivatives from Calculus. Here are the links to the refresher course on this topic:

In addition, a basic understanding of Binomial Theorem and Trigonometry would greatly help. Here are the links to the refresher courses on those two topics:

Shifting gears to $e$.

Let us consider the simple equation for compound interest: $(1 + \Large{\frac{1}{n}}$$)^n$.

If one invests a dollar that is compounded twice in a year, one would end up with:

$(1 + \Large{\frac{1}{2}}$$)^2 = 2.25$

If one invests a dollar that is compounded four times a year, one would end up with:

$(1 + \Large{\frac{1}{4}}$$)^4 = 2.44141$

Again, if one invests a dollar that is compounded twelve times a year, one would end up with:

$(1 + \Large{\frac{1}{12}}$$)^{12} = 2.61304$

Again, if one invests a dollar that is compounded 256 times a year, one would end up with:

$(1 + \Large{\frac{1}{256}}$$)^{256} = 2.71299$

Continuing this process, for a very large compounding value, the end return would stabilize at $2.71828...$

If we look at the above value it is tending towards $e$ !!!

Extending the dollar amount to $x$ implies the equation for compound interest will be: $(1 + \Large{\frac{x}{n}}$$)^n$.

Then:

$\lim_{n \to \infty} (1 + \Large{\frac{x}{n}}$$)^n = e^x$

From Binomial Theorem we know:

$(x + y)^n = {_nC_0.x^n.y^0} + {_nC_1.x^{n-1}.y^1} + {_nC_2.x^{n-2}.y^2} + ... + {_nC_{n-1}.x^1.y^{n-1}} + {_nC_n.x^0.y^n} = \sum_{k=0}^n {_nC_k} . x^{n-k} . y^k$

That is:

$(1 + \Large{\frac{x}{n}}$$)^n = 1 + \Large{\frac{n}{1!}}$ $.\Large{(\frac{x}{n})}$ $^1 + \Large{\frac{n(n-1)}{2!}}$ $.\Large{(\frac{x}{n})}$ $^2 + \Large{\frac{n(n-1)(n-2)}{3!}}$ $.\Large{(\frac{x}{n})}$ $^3 + .....$

As $n \to \infty$, all the coefficients of $n$ will tend towards $1$.

Or:

$\lim_{n \to \infty} (1 + \Large{\frac{x}{n}}$$)^n = 1 + x + \Large{\frac{x^2}{2!}}$ $+ \Large{\frac{x^3}{3!}}$ $+ .....$

In other words:

$e^x = 1 + x + \Large{\frac{x^2}{2!}}$ $+ \Large{\frac{x^3}{3!}}$ $+ .....$

Substituiting $x = i\theta$, we get:

$e^{i\theta} = 1 + i\theta + \Large{\frac{(i\theta)^2}{2!}}$ $+ \Large{\frac{(i\theta)^3}{3!}}$ $+ .....$

That is:

$e^{i\theta} = 1 + i\theta + \Large{\frac{(i\theta)^2}{2!}}$ $+ \Large{\frac{(i\theta)^3}{3!}}$ $+ \Large{\frac{(i\theta)^4} {4!}}$ $+ \Large{\frac{(i\theta)^5}{5!}}$ $+ .....$

Or:

$e^{i\theta} = 1 + i\theta - \Large{\frac{\theta^2}{2!}}$ $- \Large{\frac{i\theta^3}{3!}}$ $+ \Large{\frac{\theta^4}{4!}}$ $+ \Large{\frac{i\theta^5}{5!}}$ $- \Large{\frac{\theta^6}{6!}}$ $- \Large{\frac{i\theta^7}{7!}}$ $+ \Large{\frac{\theta^8} {8!}}$ $+ .....$

Re-arranging, we get:

$e^{i\theta} = (1 - \Large{\frac{\theta^2}{2!}}$ $+ \Large{\frac{\theta^4}{4!}}$ $- \Large{\frac{\theta^6}{6!}}$ $+ \Large {\frac{\theta^8}{8!}}$ $- .....)$ $+ i(\theta - \Large{\frac{\theta^3}{3!}}$ $+ \Large{\frac{\theta^5}{5!}}$ $- \Large{\frac {\theta^7}{7!}}$ $+ .....)$ $...\color{red}(1)$

Moving on to the next part - $sin(\theta)$.

Let us assume that we can represent $sin(\theta)$ as a polynomial series.

That is:

$sin(\theta) = a + b.\theta + c.{\theta}^2 + d.{\theta}^3 + e.{\theta}^4 + .....$ $...\color{red} (2)$

If $\theta = 0$, then we get:

$sin(0) = a + b.0 + c.{0}^2 + d.{0}^3 + e.{0}^4 + .....$

From Trigonometry, we know $sin(0) = 0$.

Therefore, we can determine the value of the coefficient $a = 0$.

Next, let us find the derivative on both sides of equation $\color{red}(2)$.

That is:

$f'(sin(\theta)) = f'(a + b.\theta + c.{\theta}^2 + d.{\theta}^3 + e.{\theta}^4 + .....)$

That is:

$cos(\theta) = b + 2.c.\theta + 3.d.{\theta}^2 + 4.e.{\theta}^3 + .....$ $...\color{red}(3)$

If $\theta = 0$, then we get:

$cos(0) = b + 2.c.0 + 3.d.{0}^2 + 4.e.{0}^3 + .....$

From Trigonometry, we know $cos(0) = 1$.

Therefore, we can determine the value of the coefficient $b = 1$.

Repeat the process of taking the derivative on both sides of the equation $\color{red}(3)$.

That is:

$f'(cos(\theta)) = f'(b + 2.c.\theta + 3.d.{\theta}^2 + 4.e.{\theta}^3 + 5.f.{\theta}^4.....)$

That is:

$-sin(\theta) = 2.c + 6.d.\theta + 12.e.{\theta}^2 + 20.f{\theta}^3.....$

If $\theta = 0$, then we get:

$-sin(0) = 2.c + 6.d.0 + 12.e.{0}^2 + 20.f{0}^3.....$

Therefore, we can determine the value of the coefficient $c = 0$.

Continuining this process, we can determine the value of the coefficient $d = -\Large{\frac{1}{6}}$ and so on.

In the end, the equation $\color{red}(2)$ can be expressed as:

$sin(\theta) = \theta - \Large{\frac{1}{6}}$ $.{\theta}^3 + \Large{\frac{1}{120}}$ $.{\theta}^5 + .....$

That is:

$sin(\theta) = \theta - \Large{\frac{\theta^3}{3!}}$ $+ \Large{\frac{\theta^5}{5!}}$ $- \Large{\frac {\theta^7}{7!}}$ $+.....$ $...\color{red}(4)$

Shifting gears on to the next part - $cos(\theta)$.

Let us assume that we can represent $cos(\theta)$ as a polynomial series.

That is:

$cos(\theta) = a + b.\theta + c.{\theta}^2 + d.{\theta}^3 + e.{\theta}^4 + .....$ $...\color{red} (5)$

Performing the same steps as we did above with $sin(\theta)$, we will get:

$cos(\theta) = 1 - \Large{\frac{\theta^2}{2!}}$ $+ \Large{\frac{\theta^4}{4!}}$ $- \Large{\frac {\theta^6}{6!}}$ $+.....$ $...\color{red}(6)$

Now to the final stage of the proof.

Compare equations $\color{red}(1)$ with equations $\color{red}(4)$ and $\color{red}(6)$ - notice a pattern ???

In other words:

$\bbox[pink,2pt] {e^{i\theta} = cos(\theta) + i.sin(\theta)}$ $...\color{red}(7)$

Substituiting $\theta = \pi$ in equation $\color{red}(7)$ above, we get:

$e^{i\pi} = cos(\pi) + i.sin(\pi)$

From Trigonometry, we know $sin(\pi) = 0$ and $cos(\pi) = -1$.

Therefore:

$e^{i\pi} = -1 + i.0$

Re-arranging the above equation, we get:

$\bbox[lightgreen,2pt] {e^{i\pi} + 1 = 0}$

BINGO - the mathematical gem of Euler's Identity !!!